The Rational Method

3. Chapter 3 of 6. THE RATIONAL METHOD

3.1 Theoretical Considerations

The Rational Method expresses a relationship between rainfall intensity and catchment area as independent variables and the peak flood discharge resulting from the rainfall as the dependent variable. It has been used for over 150 years, and known as the Rational Method for nearly 100 years. It is widely used in the design of stormwater drainage systems, farm dam spillways, and small culverts in road and railway embankments.

The detailed information of the use of the Rational Method is described in Book IV Clause 1.3.2 of ARR (2001).

The Rational Method should strictly be used for peak flow estimation only although many have assumed a simple triangular hydrograph for design. This is the case when the storm duration selected equates to the time of concentration of the catchment.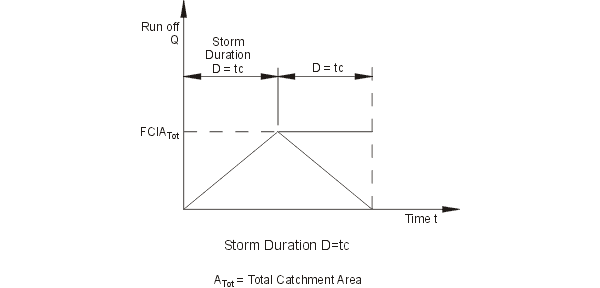

Figure 3.1 Generalised Hydrographs for the Rational Method

With the Rational Method, the assumption of uniform, steady rainfall tends towards underestimation of the peak discharge. On the other hand, neglecting storage effects within the catchment tends towards overestimation of the peak discharge. It follows that the catchments most conducive to valid results from the rational formula are those with small channel storage and short design storms (i.e. short time of concentration), since short storms tend to be more uniform in time than long ones. These constraints limit reliable applications of the rational method to urban drainage systems and small rural catchments. It should be noted that probabilistic methods described in Chapter 4 (including those derived for Western Australia) are derived from gauged catchments and hence this issue is of minor significance and outweighed by the overall accuracy limits of regionally derived methods.

Design IFD curves always show decreasing design intensities for increasing storm duration for a given average recurrence interval. In designing stormwater systems, selection of storm durations longer than the time of concentration of the catchment will always lead to lower peak discharges than storms of duration equal to tc. Analysis of design storms longer than the time of concentration of the catchment is therefore not necessary unless the stormwater drainage systems involve stormwater detention basins. With stormwater detention basins design, the combination of both runoff volume and instantaneous discharges influence the selection of storage volume and outlet discharge capacity.

Storms shorter than t_c have a higher intensity but the maximum area simultaneously contributing runoff to the peak discharge at the outlet is less than the catchment area. It is usually assumed that the reduction in contributing area outweighs the increase in rainfall intensity relative to that of a storm of duration equal to t_c and the peak discharge from the shorter storm is, therefore, the lesser. It follows that the time of concentration is normally the critical storm duration, i.e. the duration producing the highest discharge for a given average recurrence interval and runoff coefficient.

In the situations where the increase in rainfall intensity for a storm duration shorter than t_c outweighs the reduction in contributing area, the peak discharge resulting from the shorter duration storm would be higher than that generated from the storm of t_cduration. This is often referred to as the Partial Area Effect.

3.2 Application of Rational Method

3.2.1 Rural Catchments

For the rural catchments the regional formulae as specified in Section 1.4, Book IV (p16-21) of ARP: 2001 shall be used. These methods are based on the probabilitic Rational Method that is described in Chapter 4.

3.2.2 Urban Catchments

3.2.2.1.Time of Concentration
A common approach for urban catchments is to adopt t_c the summation of travel times of overland flow, gutter flow and pipe flow for the point most remote,in terms of travel time (not necessarily distance because it is a function of head loss) from the catchment outlet, i.e.

t_c = overland flow time + gutter flow time + pipe flow time

The three component times are estimated from the measured flow distances and estimated flow velocities. In each case, the velocity is an average value obtained by applying the Manning formula,

V = (R^2/3 S^1/2) / n

V = velocity (m/sec)

R = wetted perimeter (m)

S = bed slope (m/m)

n = Manning's roughness coefficient (dimensionless)

to an idealisation of the actual non-uniform and unsteady flow situation, in which the velocity varies with both time and distance. In the case of overland flow, the idealisation adopted is associated with the concept of the "kinematic wave". Central to the concept of kinematic wave is the assumption that flow velocity at any given depth is the same whether the flow is rising or falling.

For flow over plane surfaces which are homogeneous in slope and roughness, the overland flow time is given as:

t =6.94 (L  n*)^0.6 / ( I^0.4 S^0.3)  (3.3)

where:

t = overland flow time (mins)

L = flow path length (m)

n* = a surface roughness or retardance coefficient

I = rainfall intensity (mm/hr)

S = slope (m/m)

For gutter and roadway flows, the kinematic wave method is again used but the analysis is complicated by the shape of the gutter and thus a single equation such as Equation (3.3) is not available. A detailed discussion of this topic is contained in Book VIII, ARR (2000).

3.2.2.2.Determination of Flows

Flows within urban catchment shall be determined using the methodology contained in Section 1.5.5 of Book 8 of Australian Rainfall and Runoff 2001.
In particular the designer should check for partial area effects.

Guidance on runoff coefficients can be found in Table 5.4 of Special Report No. 34 Australian Road Research Board by John Argue also known as "Storm drainage design in small urban catchments".

Runoff coefficients are to be factored in accordance with Table 1.6 or ARR Book 8.

References

Australian Rainfall And Runoff; A Guide to Flood Estimation, Volume 1 2001 .
Australian Rainfall And Runoff; A Guide to Flood Estimation, Volume 2 -1987.
Argue John R.; Storm Drainage Design in Small Urban Catchments, A Hand Book for Australian Practice, Australian Road Research Board, Special Report No.34, 1987.