Overview of Hydraulic Procedures

1. Chapter 3 of 3. Overview of Hydraulic Procedures

1.1 General

Hydraulic design of waterways and associated hydraulic structures are necessary to safely and efficiently convey stormwater runoff generated from main roads and highways and to provide crossings of these roads over creeks, floodways and rivers.

Hydraulic procedures are required to compute flow characteristics in closed conduits and open channels during the passage of a runoff hydrograph. In all cases, hydraulic calculations are aimed at computing energy losses in the flow conveyance system such that the hydraulic grade line (HGL) of the system can be established. The HGL is often used to determine the location of the hydrostatic head along the water conveyance system. In the case of open channel flow, the HGL generally coincides with the water surface. In closed conduit flow conveyance systems, flow conditions can be pressurised and water rises to the HGL level at junction pits. The design process is commonly a series of iterations involving modifying the various hydraulic structures such that the resulting HGL complies with the design standards specified. These design standards can include:

• Frequency of surcharge of underground drainage systems;
• Flood levels and flow velocities along the river and floodplain;
• Flood attenuation caused by hydrograph characteristics (a function of the hydrograph shape);
• Flood attenuation caused by channel and floodplain storage (a function of the river and floodplain geometrical properties and hydraulic roughness);
• Flow directions, flood breakouts and returns, off-channel storage, etc.

In closed conduit flow conditions, calculation of energy losses within the flow conveyance system is most commonly based on applying energy loss factors to the velocity head (v2/2g). The energy loss attributed to pipe friction is best calculated by the Darcy-Weisbach Equation. Localised energy losses due to junction and inlet pits are computed in a similar manner using standard coefficients derived from extensive laboratory tests of these structures.

The simplest model available for computing flood levels and flow velocities is the use of empirical formulae such as the Chezy Equation and the Manning's Equation. These equations are referred to as slope-area methods on the basis that they utilises simple relationships between the discharge in a river to the energy gradient, flow cross-sectional area and hydraulic roughness. These formulae are suited for computing water levels only at a single location and for a single discharge value (i.e. steady flow assumptions apply) under uniform flow conditions.

These methods at best would address the second of the above five design considerations related to the hydraulics behaviour of the flow conveyance system. Often the use of slope-area methods are inappropriate due to the fact that natural river flows are not uniform.

Open channel flow conditions can often be categorised as either rapidly varying or gradually varying. Rapidly varied flow occurs whenever there is a abrupt change in the geometry of the channel or in the flow regime of the flow. In regions of rapidly varied flow, the water surface profile changes rapidly. Examples of rapidly varying flow include flow over weirs and through regions of rapid changes in bed elevation or channel width (i.e. abrupt change in geometry) and hydraulic jumps (i.e. change in flow regime). Simulations of rapidly varied flow conditions require the solution to the equations of conservation of mass and conservation of momentum in fluid flow (i.e. the Saint Venant Equations).

The flow condition generally occurring in natural river and floodplain systems can be categorised as that of gradually varied flow; that is, conditions in which the flow characteristics are non-uniform but vary gradually with distance along the channel due to gradual variation of bed slope, channel geometry and hydraulic roughness.

A number of river and floodplain computer models are available which solve either the energy equation (for steady gradually varied flow only) or the Saint Venant Equations either in its complete form or its simplified form. River and floodplain models can be categorised into the following groups:

• l-Dimensional Steady Flow Models (HECRAS, AFFLUX, and other backwater profile models);
• l-Dimensional and Quasi 2-Dimensional Unsteady Flow Models (MIKE-11, DAMBRK, DYNHYD, CELLS, TIDEWAY-2D, MIKE-12, llDEWAY-2DV. etc.);
• 2 and 3-Dimensional Unsteady Flow Models (SYSTEM-21, the TIDEWAY Suite of models etc.).

The applicability of each of the models listed is very much dependent on such factors as:

• data availability;
• resource availability (both in personnel and equipment)
• flow conditions being modelled

The sources of some of the above models are as follows:

• ​​HECRAS -​​ ​​Backwater Profile Model developed by the Hydrologic Engineering Center, US Army Corps of Engineers.
• AFFLUX - Backwater Profile Model developed by Main Roads and now available through AUSTROADS.
• MIKE-11 & 12 - Developed by the Danish Hydraulic Institute and available in Australia from Lawson and Treloar Pty. Ltd.
• DAMBRK - Developed by the US National Weather Service.
• DYNHYD - Developed by the US Environment Protection Agency and available in Australia from Willing and Partners Pty. Ltd.
• CELLS - Developed originally in the University of Witwatersrand in South Africa and modified by various organisations in Australia to improve stability and computation efficiency (ref. Monash University).
• MIKE-21 - Developed by the Danish Hydraulic Institute and available in Australia from Lawson and Treloar Pty. Ltd.
• TlDEWAY - The TIDEWAY suite of models were developed by Hydraulic Research Limited in Wallingford, UK and are available in Australia from Patterson Britton and Partners Pty. Ltd. The Suite of programs consist of TIDEWAY-1D, TIDEWAY-2D, TIDEWAY-2DV, TIDEWAY-3D and TIDEMEAN-3D.

The applicability of each of the models listed is very much dependent on such factors as:

• data availability;
• resource availability (both in personnel and equipment); and
• flow conditions being modelled.
  
  

1.2 Darcy-Weisbach Equation

For closed conduit operating under full flow conditions (either pressurised or non-pressurised), the energy loss associated with the pipe friction is best computed by the Darcy-Weisbach Equation, expressed as follows:-

Where

hL	is the energy loss along the length of the pipe (m)
f	is the friction factor which is dependent on the type of pipe, its diameter and the flow Reynolds Number. The appropriate value of f can be read from the standard "Moody Diagram"
L	is the length of the pipe (m)
D	is the diameter (or equivalent diameter) of the pipe
v	is the flow velocity within the pipe (m/s)
g	is the gravitational acceleration (m/s2)

For localised energy losses associated with junction and inlet pits, the term fL/D in equation (3.1) is replaced by a head loss coefficients derived from standard charts resulting from various laboratory studies, particular the "Missouri Charts" which were based on extensive laboratory studies by Sangster et al. (1958) from the University of Missouri.

1.3 Slope-Area Methods

Slope-area methods are useful in providing a quick means of determining flows. They are particularly useful when estimating historical flows from flood marks. Equations commonly used include the Manning's Equation and the Chezy Equation as expressed in Equations (3.2) and (3.3) respectively.
and

Where​​	Q	is the discharge (m3/s)
	A	is the area of the flow cross section (m2)
	R	is the hydraulic radius of the flow section and is the ratio of the flow area to the wetted perimeter (m)
	Sf	is the friction slope, often approximated by the bed slope of the channel
	n	is the Manning's roughness coefficient
	C	is the Chezy roughness coefficient

It is evident that the two equations are similar and both equations assume uniform one-dimensional flow conditions.

1.4 One-Dimensional Steady Flow Models

Steady flow hydraulic models, as the name implies, are confined to applications in situations of steady or gradually varied flow. These types of model are often easy to use and are based on simple hydraulic calculations using the principle of conservation of energy to compute flood levels. The most common of the steady flow one-dimensional models is HECRAS (US-Army Corps of Engineers) and AFFLUX (Main Roads). Steady flow models are restricted to modelling river and floodplain systems under the following conditions:

• The flood hydrograph is generally of long duration with a slow rate of rise (i.e. gradually varied) such that attenuation effects are less dominant and backwater effects have the most significant influence on flood levels;
• The slope of the river reach is less than 1 in 10;
• There is no significant wide expansive floodplain which could significantly attenuate the flood hydrograph. If storage attenuation effects are significant, it may be necessary to first compute the attenuated flow (by runoff routing perhaps) before proceeding with the hydraulic model.

Steady flow models are normally one-dimensional, although models such as HECRAS have some quasi-two-dimensional capabilities with 'split-flow' option.

Steady flow one-dimensional models can also be used to model flow characteristics in a network system or a braided channel system. Models such as HECRAS can be used in a fairly creative manner to compute flood levels in reasonably complex river networks.

Field data requirements for this type of model are river cross-sections and dimensions of special structures (bridges, culverts, weirs, etc.) likely to cause backwater effects. The main model parameters are the roughness coefficients, and flow contraction and expansion coefficients. In HECRAS, the use of the split flow option would also require weir flow coefficients for the overtopping sections.

1.5 One-Dimensional Unsteady Flow Models

Applications of one-dimensional flow models are common in the industry and are generally quite appropriate for most river flood studies. Quite often, it is the assumption of steady or gradually varied flow (or the insignificance of flood attenuation) rather than limitations of one-dimensional flow assumptions that inhibits the wider application of steady one-dimensional flow models. Unsteady flow models are generally more rigorous, using the momentum and continuity equations to compute the significance of hydrograph and storage characteristics on flood attenuation. Unsteady flow models can be classified into groups dependent upon the extent to which these models solve the equations of motion. Briefly, the momentum equation contains both the convective acceleration and local acceleration terms. In most natural rivers under normal flood conditions, the local acceleration term is usually an order of magnitude lower than the convective acceleration term. This has led to many models leaving the local acceleration out of the equation of motion to improve model stability and relax the maximum space and time increment requirements.

Models such as MIKE-11, DYNHYD and CELLS fall into this group of unsteady flow models. MIKE-11 has the option of removing or reinstating the local acceleration term.

In a situation where the shape of the flood hydrograph is 'peaky', that is when flow conditions are rapidly varied (such as in an road embankment failure event), the additional local acceleration term becomes significant. Models such as DAMBRK and MIKE-11 are equipped to model such situations.

1.6 Quasi-two Dimensional Models

Even in gradually varied flow conditions, the occurrence of flood breakouts and floodplain pondage in a channel/floodplain flow situation can have a significant influence on the attenuation/reduction of flow in the channel. This has led to the development of quasi two-dimensional models, aimed at a 'compromised' modelling structure of a fairly rigorous hydraulic computation in the primary flow direction (i.e. along the channel) and some accounting for lateral flow characteristics and floodplain pondage. The lateral connection between cells or nodes are often by simple weir or channel flow formulae.
There is a further type of quasi two-dimensional model for water quality modelling in rivers. These models are 'two-dimensional' in the vertical axis to model such stratified flow phenomena as salt intrusion. Such models include MIKE-12 and TIDEWAY-2DV.

Data requirements for this type of model are similar to those for the steady flow models. If the quasi two-dimensional approach is adopted, additional survey data on the ground profile at the lateral flow connections and dimensions of the side channel will be needed.

1.7 Two and Three-Dimensional Models

Full two and three-dimensional models solve the equation of motion in all directions of flow. They are by far the most rigorous but also require the most ground information to compute flow characteristics reliably. Two-dimensional models have been used to study localised hydraulic effects such as occur in the vicinity of bridge crossings. Owing to the rigorous nature of such models, computation can be time consuming and require high speed computers (which are becoming more and more readily available). Figure 3.1 is a schematic diagram of results from a two-dimensional model.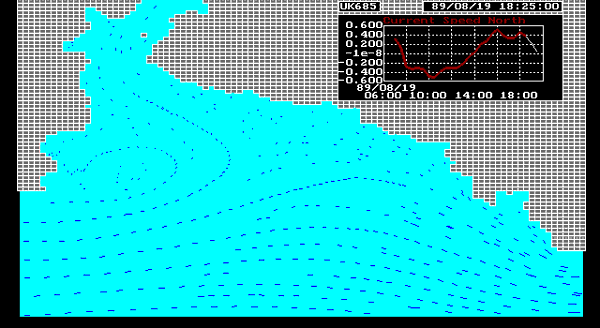

Figure 3.1 Typical Output from MIKE-21

Three-dimensional models are not often applied to river and floodplain studies and are mainly used in ocean and estuary studies. They feature in water quality modelling investigation where variation of water pollutants is dependent on flow distribution (x and y directions) and density (z direction).

 

Reference

Australian Rainfall And Runoff;(1987), A Guide to Flood Estimation, Volume I & II.

Sangster, W.M., Wood, H.M., Smerdon, E.T. and Bossy, H.G., (1958), Pressure Changes at Storm Drain Junctions, Engineering Series Bulletin No. 41, Engineering Experiment Station, University of Missouri.